|
DisCont
Program DisCont jest interfejsem pomiędzy systemem operacyjnym Windows a programami CONTIN i DISCRETE.
Program CONTIN został napisany przez S.W. Provenchera i przeznaczony jest między innymi do analizy (fitowania) danych eksperymentalnych z użyciem ciągłych rozkładów w szukanych parametrach.
DISCRETE również autorstwa S. W. Provenchera analizuje dane i proponuje model oparty na dyskretnych wartościach parametrów.
W obu programach nie jest wstępnie określona liczba spodziewanych składowych.
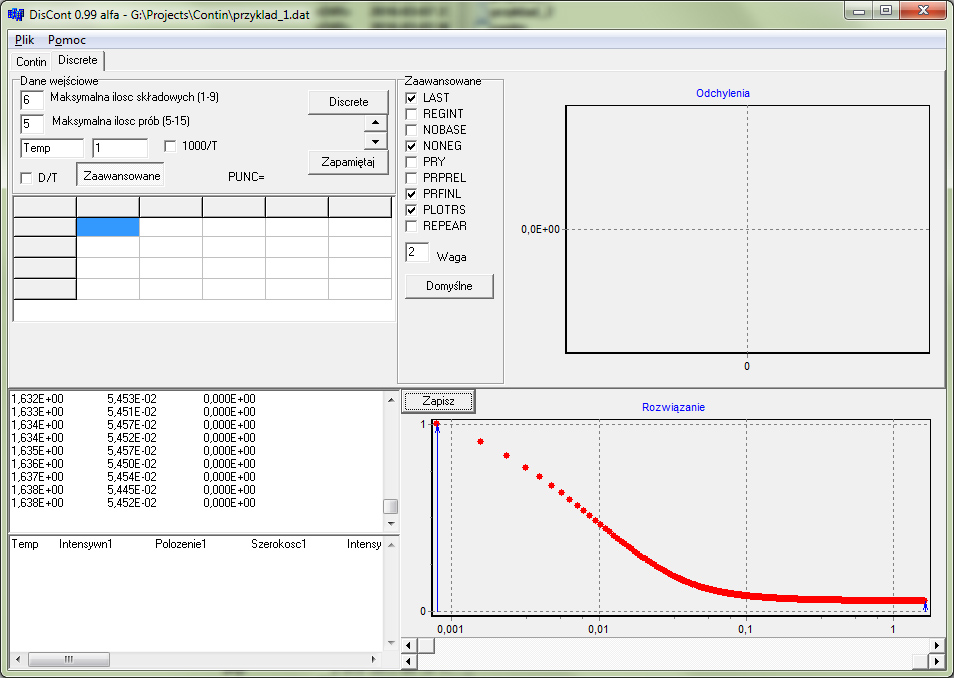
Program DisCont przeznaczony jest do przeglądania, prezentacji graficznej i manipulacji danych, a także do przygotowania pliku configuracyjnego *.in wymaganego przez programy wykonywalne CONTIN i DISCRETE. Po uruchomieniu wybranego programu wyniki obliczeń są prezentowane w formie graficznej i tekstowej. Program DisCont sugeruje najbardziej prawdopodobne rozwiązanie, ale istnieje możliwość przeglądania i wybór dowolnego z obliczonych rozwiązań. Akceptowane rozwiązania w obrębie serii pomiarowej wraz z innymi parametrami mogą być gromadzone w formularzu rozwiązań, który po zapisie do pliku jest łatwo importowany do innych zewnętrznych programów (np. Origin). Treść okna graficznego z danymi wejściowymi i aktualnym dopasowaniem może być przepisana na formularz tekstowy w celu wyeksportowania rezultatów obliczeń do pliku.
|
|
|
Program należy rozpakować do dowolnego folderu.
W archiwum znajduje się mini pomoc do programu oraz przykładowe pliki danych. Podczas działania programu pliki z danymi muszą znajdować się w folderze z programem. Wymaganym separatorem dziesiętnym jest kropka, którą można ustawić w opcjach regionalnych i językowych systemu operacyjnego.
DisCont -
DOWNLOAD
Liczba pobrań:
1108
Wszelkie pytania i uwagi proszę kierować na adres:
marek.kempka@amu.edu.pl
Literatura:
Provencher S.W., A constrained regularization method for inverting data represented by lineair algebraic or integral equations, Computer Physics Communications, 27(3), 213-227 (1982)
Provencher S.W., CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations, Computer Physics Communications, 27(3), 229-242 (1982)
http://s-provencher.com
|